Motivation
The engagement with a fascinating geometric problem involving the creation of a three-dimensional solid model can be traced back to the 18th century: The goal is to find a solid that has a circular base, looks like a triangle from one side, and like a square from the other. The appeal of the problem has not diminished over the years; Mathematicians and mathematics educators are still engaged with similar or slightly modified versions of it.
Peter Friedrich Catel was the first, who described the problem in his book “Mathematisches und physikalisches Kunst-Cabinet” in 1790 [1]. As a precision mechanic and toy manufacturer from Berlin, he crafted a board made of plum wood, which was equipped with three openings and is referred to as “The Mathematical Openings” [5].
Historical Background
Despite the addressed solution to this problem in the aforementioned book the Hungarian mathematician George Pólya revisited the problem 200 years later in his book “How to Solve It” in 1966. In it, the sought-after solid is referred to as a universal plug [2, p. 200]. The problem is formulated in a very similar manner. Therefore, three conditions are given which the sought solid must apply [2, pp. 200]. In our contribution we follow this description of the problem, and we call the sought-after solid “universal plug” such as other authors before [3, 4]. However, as the name might suggest, there is no unique solution. Echoing the mentioned historical instances, the problem hints at a singular solution. In fact, there are infinitely many solids that satisfy the mentioned conditions.
Mathematical Background
In our contribution we investigate the possibility of multiple solids satisfying the geometric problem's specified conditions. We aim to identify and compare the volumes of these qualifying solids. Assuming, that we limit ourselves to convex solids, these can be ordered by their volume. Thus, a solid with the minimal volume and a solid with the maximal volume can be found, which can be considered as the boundaries of a continuum within which all convex solutions can be identified.
Comparison of methods (against the background of learning environments)
The approaches to volume determination of these solids can be illustrated through the creation of models using different methods. As a tactile method to illustrate the infinite number of solutions, shaping the models with modeling clay based on a framework with the three shapes (circle, square, triangle) is suggested. A suitable analog method to create the universal for younger learns is the use of playdough. A framework made of cardboard helps also modelling different versions of the universal plug such as the one of maximal volume. As an analog method creating a universal plug of minimal volume, layering cardboard cuts is recommended. Both methods are suitable for learners of all ages to deal with the given problem.
Of course, 3D printing can be one suitable approach. Especially in computer-based learning environments it might be the best option. One handy software is “3D Builder”, which is easy to use for younger learners. A 3D model of the universal plug of maximum volume could be designed easily in this way (see Fig. 1). A 3D model of the universal plug of minimum volume is much more difficult to design and requires the use of a different program such as “Thinker CAD”. In our contribution we describe all approaches of modelling different solids and compare advantages of the different methods against the background of suitable learning environments for learners of different ages.
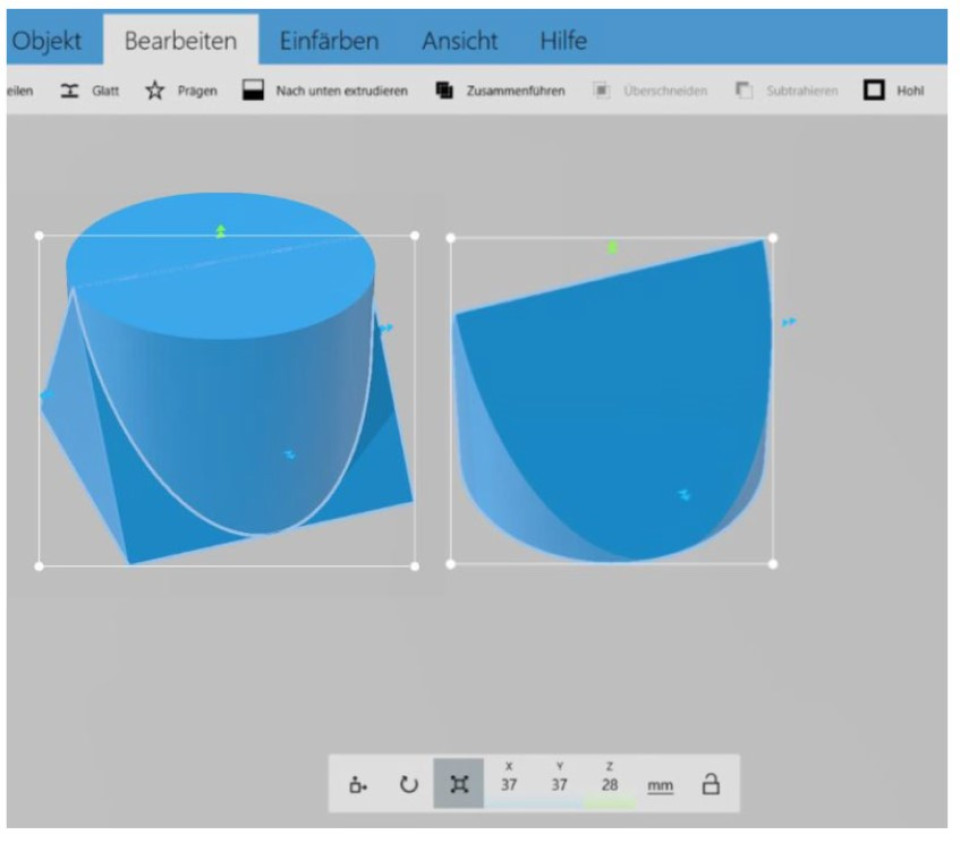
Fig. 1. Using Microsoft 3D Builder to design a universal plug of maximum volume.
References
1. Catel, P.: Mathematisches und physikalisches Kunst-Cabinet, dem Unterrichte und der Belustigung der Jugend gewidme. Berlin (1790).
2. Pólya, G.: Vom Lösen mathematischer Aufgaben. Einsicht und Entdeckung, Lernen und Lehren. Springer, Basel (1966)
3. Müller, M., Poljanskij, N.: Gibt es mehr als einen Pólya-Stöpsel? Verschiedene Zugänge zu einer geometrischen Problemstellung. In: Sjuts, J., Vásárhelyi, É. (eds.), Theoretische und empirische Analysen zum geometrischen Denken, pp. 227– 242. WTM, Münster (2021).
4. Neubrand, M.: Mathematik zu einem Spielzeug. Didaktik der Mathematik 13, 63-73 (1985).
5. Stauss, T.: Frühe Spielwelten. Zur Belehrung und Unterhaltung. Die Spielwarenkataloge von Peter Friedrich Catel (1747-1791) und Georg Hieronimus Bestelmeier (1764-1829). Librum, Hochwald (2015).

